La psychométrie est la science qui étudie les techniques de mesures pratiquées en psychologie, ainsi que les techniques de validation et d’élaboration de ces mesures. ComColors a fait le choix d’une psychométrie très rigoureuse pour garantir la robustesse de son modèle et la fiabilité de ses résultats.
Cet article vous présente en détails les résultats de la recherche psychométrique du modèle ComColors.
La stabilité temporelle de l’échelle ComColors
La stabilité est un critère de fidélité qui permet d’apprécier si une échelle reste fiable dans le temps. L’indicateur statistique qui permet de mesurer la stabilité est la corrélation. Pour être considérées comme stables les réponses d’une même personne doivent être les mêmes quand elle répond deux fois aux mêmes questions. Si elle ne répond pas de manière stable cela veut dire que la mesure de l’échelle est trop éphémère pour être utilisée. Le seuil admis en matière de stabilité est de .70. Globalement les items de l’échelle doivent atteindre ou dépasser ce seuil.
Les corrélation test/retest pour l’ensemble des couleurs sont les suivantes :
| Couleur | Corrélation test/retest |
|---|---|
| Rouge | 0.72 |
| Orange | 0.79 |
| Jaune | 0.70 |
| Vert | 0.74 |
| Bleu | 0.75 |
| Violet | 0.72 |
Ces corrélations sont toutes supérieures à .70 qui est le seuil recommandé permettant d’estimer si une échelle est stable, il est donc possible de conclure que toutes les couleurs du modèle ComColors présentent un coefficient de stabilité tout à fait acceptable.
Analyse factorielle exploratoire
La validation psychométrique du questionnaire ComColors a été élaborée sous la direction d’un docteur en psychologie qui a appliqué les méthodologies psychométriques actuelles en utilisant les outils de recherche les plus récents à ce jour (2012).
La première étape a été de créer un questionnaire qui permette de réaliser une analyse factorielle exploratoire. Ce travail a consisté à mesurer les dimensions psychologiques des six types de personnalité du modèle ComColors. Pour réaliser ce travail, il a été nécessaire de créer une première série de questions que nous avons soumise à un groupe d’environ 130 personnes. Ainsi, nous avons pu distinguer les dimensions psychologiques fiables de celles qui ne donnaient pas lieu à des mesures de qualité. Nous avons renouvelé quatre fois cette opération pour réussir à obtenir une mesure claire des dimensions psychologiques mesurées.
Le tableau ci-dessous est le résultat de la dernière analyse factorielle exploratoire qui montre que conformément aux attentes les items d’une dimension (bleu par exemple) ne sont fortement saturés qu’avec un seul facteur et très faiblement avec les facteurs des autres dimensions.
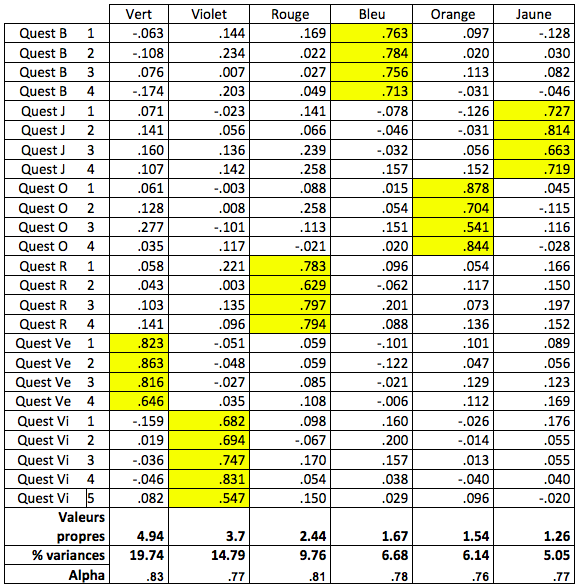
À l’issue de cette dernière analyse factorielle exploratoire (AFE), nous avons entrepris une validation plus approfondie de la structure du questionnaire en réalisant une analyse factorielle confirmatoire (AFC) sur 352 participants. L’analyse factorielle confirmatoire est une technique statistique qui se situe dans le prolongement de l’analyse factorielle exploratoire. Le but de l’Analyse Factorielle Confirmatoire est de tester la solidité du modèle théorique que l’on a réussi à faire émerger dans l’analyse exploratoire. L’AFC est donc une étape beaucoup plus avancée dans la démarche de recherche que l’AFE.
Analyse factorielle confirmatoire
Le principe de l’analyse confirmatoire est de vérifier si le modèle théorique n’est pas différent du modèle observé. Afin de vérifier cette absence de différence, des indicateurs sont calculés afin de mesurer la qualité de l’ajustement entre le modèle théorique et le modèle observé.
Le premier indicateur à prendre en compte est le χ2 car il permet de calculer l’existence d’un écart entre la matrice de covariance observée et la matrice de covariance estimée. Si l’idéal est d’accepter l’hypothèse nulle ce test pose problème car il est dépendant de l’effectif de l’échantillon et du nombre de paramètres du modèle testé. Pour éviter ces distorsions, l’interprétation de différents indicateurs vise à obtenir une meilleure estimation de la qualité de l’ajustement.
Dans cette recherche nous avons retenu un certain nombre d’indicateurs d’ajustement qui sont communément admis pour vérifier la qualité du modèle observé.
Le CFI (Comparative Fit Index) et le TLI (Tucker-Lewis Index) sont des indicateurs qui sont basés sur l’écart au modèle d’indépendance. Ces indicateurs examinent la différence entre le chi2 du modèle testé et le chi2 du modèle théorique. Leur valeur peut varier théoriquement de 0 à 1. On considère qu’ils indiquent un bon ajustement à partir de valeurs de l’ordre de .90.
Le RMSEA (Root Mean Square Error of Approximation) permet d’évaluer les écarts normalisés entre la matrice observée et la matrice estimée. Les auteurs considèrent qu’une valeur égale ou inférieure à .06 est le gage d’un bon ajustement.
Une dernière catégorie d’indicateur se focalise sur la variance expliquée. Le SRMR standardisé (Standardized Root Mean Residual) est la racine carrée de la moyenne de la somme des carrés des résidus de chaque cellule de la matrice. Les auteurs considèrent qu’une valeur égale ou inférieure à .05 est le signe d’un bon ajustement.
Le GFI (« Goodness of Fit Index ») permet de prendre en compte la variance de la matrice observée sur laquelle s’appuie le modèle. Cet indicateur varie théoriquement entre 0 et 1, avec une valeur des ajustements au moins égale à .90.

Comme nous pouvons le constater sur le tableau ci-dessus tous les indicateurs d’ajustement atteignent et généralement dépassent les seuils recommandés, il est donc justifié de dire que le modèle ComColors s’ajuste correctement aux données et il peut donc être considéré comme valide d’un point de vue structurel.
Le travail de recherche qui soutient le modèle ComColors a été pensé et entretenu afin de garantir la robustesse de son modèle et la fiabilité de ses résultats.
Dernière mise à jour le 19 février 2024